三级片视频播放,精品三级片在线观看,A级性爱视频,欧美+日韩+国产+无码+小说,亲子伦XX XX熟女,秋霞最新午夜伦伦A片黑狐,韩国理伦片漂亮的保拇,一边吃奶一边做边爱完整版,欧美放荡性护士videos

一、模糊控制概況

模糊邏輯控制(Fuzzy Logic Control)簡稱模糊控制(Fuzzy Control)，是以模糊集合論、模糊語言變量和模糊邏輯推理為基礎的一種計算機數字控制技術。1965年，美國的L.A.Zadeh創立了模糊集合論；1973年他給出了模糊邏輯控制的定義和相關的定理。1974年，英國的E.H.Mamdani首先用模糊控制語句組成模糊控制器，并把它應用于鍋爐和蒸汽機的控制，在實驗室獲得成功。這一開拓性的工作標志著模糊控制論的誕生。

模糊控制實質上是一種非線性控制，從屬于智能控制的范疇。模糊控制的一大特點是既具有系統化的理論，又有著大量實際應用背景。模糊控制的發展最初在西方遇到了較大的阻力；然而在東方尤其是在日本，卻得到了迅速而廣泛的推廣應用。近20多年來，模糊控制不論從理論上還是技術上都有了長足的進步，成為自動控制領域中一個非常活躍而又碩果累累的分支。其典型應用的例子涉及生產和生活的許多方面，例如在家用電器設備中有模糊洗衣機、空調、微波爐、吸塵器、照相機和攝錄機等；在工業控制領域中有水凈化處理、發酵過程、化學反應釜、水泥窯爐等的模糊控制；在專用系統和其它方面有地鐵靠站停車、汽車駕駛、電梯、自動扶梯、蒸汽引擎以及機器人的模糊控制等。

二、模糊控制基礎

模糊控制的基本思想是利用計算機來實現人的控制經驗，而這些經驗多是用語言表達的具有相當模糊性的控制規則。模糊控制器(Fuzzy Controller，即FC)獲得巨大成功的主要原因在于它具有如下一些突出特點：

• 模糊控制是一種基于規則的控制。它直接采用語言型控制規則，出發點是現場操作人員的控制經驗或相關專家的知識，在設計中不需要建立被控對象的精確數學模型，因而使得控制機理和策略易于接受與理解，設計簡單，便于應用。

• 由工業過程的定性認識出發，比較容易建立語言控制規則，因而模糊控制對那些數學模型難以獲取、動態特性不易掌握或變化非常顯著的對象非常適用。

• 基于模型的控制算法及系統設計方法，由于出發點和性能指標的不同，容易導致較大差異；但一個系統的語言控制規則卻具有相對的獨立性，利用這些控制規律間的模糊連接，容易找到折中的選擇，使控制效果優于常規控制器。

• 模糊控制算法是基于啟發性的知識及語言決策規則設計的，這有利于模擬人工控制的過程和方法，增強控制系統的適應能力，使之具有一定的智能水平。

• 模糊控制系統的魯棒性強，干擾和參數變化對控制效果的影響被大大減弱，尤其適合于非線性、時變及純滯后系統的控制。

模糊控制系統的基本結構如圖1所示：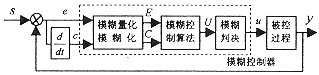

圖1　模糊控制系統框圖

其中s為系統的設定值，y為系統輸出，e和c分別是系統偏差和偏差的微分信號，也就是模糊控制器的輸入，u為控制器輸出的控制信號，E、C、U為相應的模糊量。由圖可知模糊控制器主要包含三個功能環節:用于輸入信號處理的模糊量化和模糊化環節，模糊控制算法功能單元，以及用于輸出解模糊化的模糊環節。

模糊控制器設計的基本方法和主要步驟大致包括：

1、選定模糊控制器的輸入輸出變量，并進行量程轉換。選取方法一般如圖1所示，即分別取e、c和u。

2、確定各變量的模糊語言取值及相應的隸屬函數，即進行模糊化。模糊語言值通常選取3、5或7個，例如取為{負，零，正}，{負大，負小，零，正小，正大}，或{負大，負中，負小，零，正小，正中，正大}等。然后對所選取的模糊集定義其隸屬函數，可取三角形隸屬函數(如圖2所示)或梯形，并依據問題的不同取為均勻間隔或非均勻的；也可采用單點模糊集方法進行模糊化。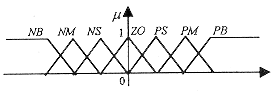 

圖2　隸屬函數取法示意

3、建立模糊控制規則或控制算法。這是指規則的歸納和規則庫的建立，是從實際控制經驗過渡到模糊控制器的中心環節。控制律通常由一組if-then結構的模糊條件語句構成，例如:if e=N and c=N，then u=PB……等；或總結為模糊控制規則表，如表1中所示，可直接由e和c查詢相應的控制量u。

表1 模糊控制規則表舉例

4、確定模糊推理和解模糊化方法。常見的模糊推理方法有最大最小推理和最大乘積推理兩種，可視具體情況選擇其一：解模糊化方法有最大隸屬度法，中位數法，加權平均，重心法，求和法或估值法等等，針對系統要求或運行情況的不同而選取相適應的方法，從而將模糊量轉化為精確量，用以實施最后的控制策略。